Равномерное движение
1) Средняя скорость
$$\boxed{\vec{V} = \frac {\vec S} t \text{ [м/с]}} $$
$$\vec{V} - \text{средняя скорость (м/с)} $$
$$\vec S - \text{перемещение (м)} $$
$$t - \text{время за которое сделано перемещение (с)} $$
2) Среднепутевая скорость
$$\boxed{{V} = \frac {L} t \text{ [м/с]}}$$
$$V - \text{среднепутевая скорость (м/с)}$$
$$L - \text{путь (м)}$$
$$t - \text{время (с)}$$
3) Зависимость координат от времени при равномерном прямолинейном движении
$$\boxed{X(t) = X_{0} + V_x \cdot t \text{ [м]}}$$
$$X - \text{конечная координата тела (м)}$$
$$X_{0} - \text{начальная координата тела (м)}$$
$$V_{x} \text{ - конечная скорость тела (м/с)} $$
$$t \text{ - время (с) } $$
Равноускоренное движение
4) Ускорение
$$\boxed{\vec{a} = \frac {\vec Vк- \vec Vн} t \text{ [м/с²]}}$$
$$\vec{a} - \text{ускорение (м/с²)} $$
$$\vec Vк - \text{конечная скорость (м/с)} $$
$$\vec Vн - \text{начальная скорость (м/с)} $$
$$t -\text{ время(с)} $$
5) Зависимость координат от времени при равноускоренном движении
$$\boxed{X(t) = X_{0} + V_{0_{x}}\cdot t + {{a_{x} \cdot t^2 \over 2}} \text { [м]}}$$
$$X \text{ - конечная координата тела (м)} $$
$$X_{0} - \text{начальная координата тела (м)}\\$$
$$V_{0_{x}} - \text{начальная скорость тела (м/с)}$$
$$t \text{ - рассматриваемый промежуток времени (с) } $$
$$a_{x} - \text{ускорение (м/с²)} $$
6) Перемещение при равносукоренном движении (три формулы)
$$\boxed{ S_{x} = {V_{К_{x}}^2 - V_{0_{x}}^2 \over 2a_{x}} \text { [м]}}$$
$$S_{x} - \text{перемещение(м)} $$
$$V_{К_{x}} - \text{конечная скорость тела (м/с)} \\ $$
$$V_{0_{x}} - \text{начальная скорость тела (м/с)}\\ $$
$$a_{x} - \text{ускорение (м/с²)} \\ $$
$$ \boxed{S_{x} = {V_{К_{x}} + V_{0_{x}} \over 2} \cdot t \text{ [м]}}$$
$$S_{x} - \text{перемещение(м)} $$
$$V_{0_{x}} - \text{начальная скорость тела (м/с)} $$
$$V_{К_{x}} \text{ - конечная скорость тела (м/с) } $$
$$t - \text{Время} (с) $$
$$\boxed{ S_{x} = V_{0_{x}}\cdot t + {{a_{x} \cdot t^2 \over 2}} \text { [м]}}$$
$$S_{x} - \text{перемещение(м)} $$
$$V_{0_{x}} - \text{начальная скорость тела (м/с)}\\$$
$$a_{x} - \text{ускорение (м/с²)} \\$$
$$t - \text{рассматриваемый промежуток времени (с) } \\$$
7) Зависимость скорости от времени при равноускоренном движении
$$\boxed{ V_x(t) = V_{0_{x}} + {{a_{x} \cdot t}} \text { [м/c]}}\\$$
$$V_{0_{x}} - \text{начальная скорость тела (м/с)}$$
$$a_{x} - \text{ускорение (м/с²)} $$
$$t \text{ - рассматриваемый промежуток времени (с) } $$
$$V_{x} \text{ - конечная скорость тела (м/с)} $$
Динамика
8) Первый закон Ньютона (формулировка)
$$Первый \ закон \ Ньютона \text{ - существуют системы отсчëта, в которых тело покоится или движется равномерно прямолинейно при отсутствии действия на него сил. Такие системы называются инерциальными.} $$
9) Второй закон Ньютона
$$ \boxed{\vec{a} = \frac {\vec F} m\text{ [м/с²]}}$$
$$ \vec{a} - \text{ускорение тела (м/с²)} $$
$$ \vec {F} - \text{сумма всех сил действующих на тело, (H)} $$
$$m - \text{масса тела (кг)} $$
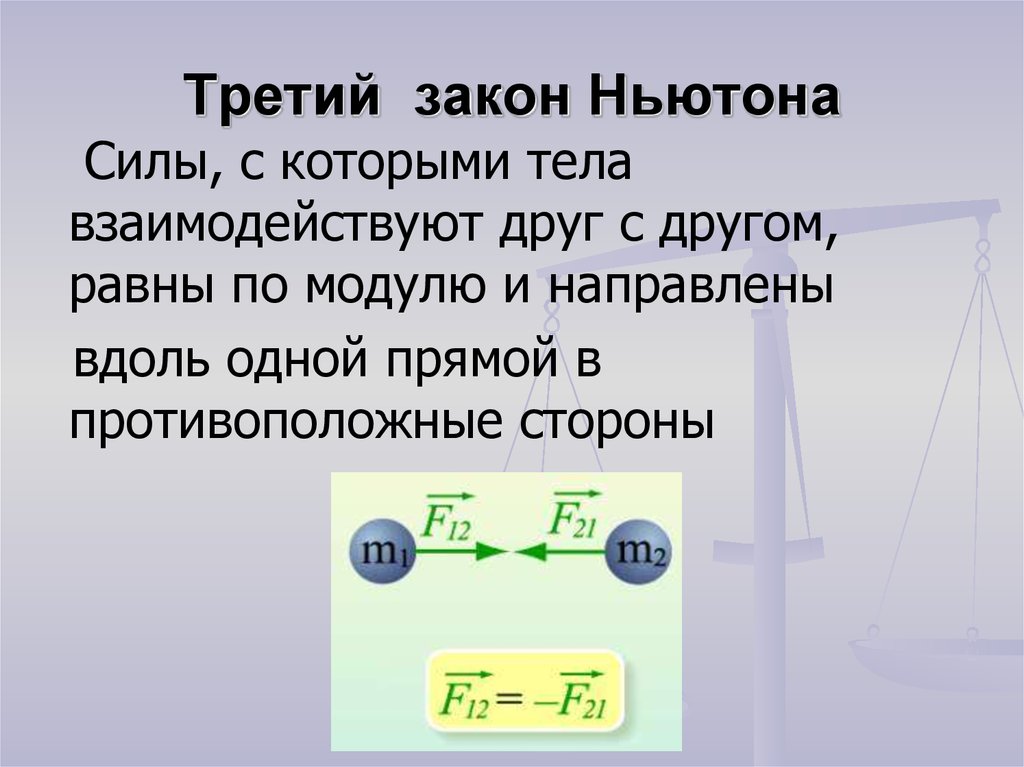
10) Третий закон Ньютона (рисунок)
$$ \boxed{\vec{F_{1_{2}}} = \vec{ -{F_{2_{1}}}}}$$
$$ \vec{F_{1_{2}}} - \text{сила, действующая на первое тело со стороны второго тела (H)} $$
$$ \vec{ -F_{2_{1}}} - \text{сила, действующая на второе тело со стороны первого (H)} $$
Третий закон Ньютона - при взаимодействии двух тел возникает пара сил, которые
1. равны по модулю
2. направлены вдоль одной прямой
3. противоположены по направлению
4. силы одной природы
11) Закон гравитационного взаимодействия (без векторов)
$$ \boxed{{F} = {{G} } \cdot{m_{1} \cdot m_{2} \over r^2 } \text{ [H]}}$$
$$ {F} - \text{сила гравитационного взаимодействия (H)} $$
$$ {G} - \text{гравитационная постоянная (H · м² / кг² )} $$
$$ m_{1} , m_{2} - \text{масса взаимодействующих тел (кг)} $$
$$ r - \text{ расстояние между центрами масс тела (м)} $$
12) Сила тяжести
$$ \boxed{\vec{F} = {m} \cdot {\vec{g}} \text{ [H]}}$$
$$ \vec{F} - \text{сила тяжести (H)} $$
$$ m - \text{ масса тела (кг)} $$
$$ {\vec{g}} - \text{ускорение свободного падения (м/с²)} $$
13) Сила упругости
$$ \boxed{{\vec{F}_{упр}} = {-k} \cdot {\Delta\vec{l}} \text{ [H]}}$$
$$ {\vec{F}_{упр}} - \text{сила упругости (H)} $$
$$ {k} - \text{коэффициент жесткости тела (H/м)} $$
$$ {\Delta\vec{l}} - \text{изменение длины пружины (м)} $$
14) Сила трения скольжения
$$ \boxed{{{F}_{тр}} = {μ} \cdot {N} \text{ [H]}}$$
$$ {{F}_{тр}} - \text{сила трения (H)} $$
$$ {μ} - \text{коэффициент трения} $$
$$ N - \text{сила реакции опоры (H)} $$
15) Архимедова сила
$$ \boxed{{\vec{F}_{арх}} = {-ρ} \cdot {\vec{g}} \cdot {V_{погруж}}\text{ [H]}}$$
$$ {\vec{F}_{арх}} - \text{сила Архимеда (H)} $$
$$ {ρ} - \text{плотность жидкости или газа (кг/м³)} $$
$$ {\vec{g}} - \text{ускорение свободного падения (м/с²)} $$
$$ V_{погруж} - \text{ объем погруженной части тела (м³)} $$
Статика
16) Момент силы
$$ \boxed{M = {F \cdot L} \text{ [Н · м]}} $$
$$M - \text{момент силы (Н · м)}$$
$$F - \text{сила (Н)} $$
$$L - \text{расстояние от точки оси вращения до линии действия силы (м)} $$
17) Условия равновесия протяжённого твёрдого тела
$$\text{1) Векторная сумма всех сил, действующих на тело равно 0 . } $$
$$\boxed{\sum_{\iota=1}^n{\vec F_{\iota}}={\vec 0}}$$
$$\text{2) Сумма всех моментов, закручивающих рычаг по часовой стрелке, равно сумме всех моментов, закручивающих рычаг против часовой стрелке.} $$
$$\boxed{\sum_{\iota=1}^n{M}={0}}$$
18) Коэффициент полезного действия
$$ \boxed{η = {{A_{полез} \over A_{затр}}} \ \cdot 100\% } $$
$$η - \text{К.П.Д. (%)}$$
$$A_{полез} - \text{полезная работа (Дж)}$$
$$A_{затр} - \text{вся затраченная работа (Дж)}$$
19) Давление
$$ \boxed{P = {F_{⟂} \over S} \text{ [Па]}} $$
$$ P - \text{давление (Па)}$$
$$F_{⟂} - \text{сила, действующая перпендикулярно к поверхности (Н)} $$
$$S - \text{площадь поверхности (м²)} $$
20) Плотность
$$ \boxed{{ρ} = {{m} \over {V}}\text{ [кг/м³]}}$$
$$ {ρ} - \text{плотность вещества (кг/м³)} $$
$$ m - \text{масса вещества (кг)}$$
$$ {V} - \text{ объем вещества (м³)}$$
21) Средняя плотность
$$ \boxed{{ρ} = {{m_{вся}} \over {V_{весь}}}\text{ [кг/м³]}}$$
$$ {ρ} - \text{средняя плотность (кг/м³)} $$
$${m_{вся}} - \text{вся масса тела (кг)}$$
$${V_{весь}} - \text{весь объем тела (м³)}$$
22) Гидростатическое давление
$$ \boxed{P = {ρ \cdot g \cdot h} \text{ [Па]}} $$
$$ P - \text{давление (Па)}$$
$$ρ - \text{плотность жидкости (кг/м³)} $$
$$g - \text{ускорение свободного падения (м/с²)} $$
$$h - \text{расстояние от исследуемой точки до свободной поверхности жидкости (м)} $$
23) Закон Паскаля (формулировка)
$$Закон \ Паскаля \text{ - Давление, производимое на жидкость или газ, передаëтся одинаково по всем направлениям.} $$
24) Закон гидравлического пресса
$$\boxed{{F_{1}\over {F_{2}}} = {S_{1}\over S_{2}} = {h_{2}\over h_{1}}}$$
$${F_{1}},{F_{2}} - \text{силы, действующие на поршни (Н)}$$
$${S_{1}},{S_{2}} - \text{площади поршней (м²)}$$
$$h_{1},{h_{2}} - \text{расстояния, на которые поршни смещаются (м)} $$
25) Условие плавания тел
$$ \boxed{F_{арх} \gt F_{тяжести}} \text{ тело всплывает}$$
$$ \boxed{F_{арх} = F_{тяжести}} \text{ тело плавает}$$
$$ \boxed{F_{арх} < F_{тяжести}} \text{ тело тонет}$$
$$ {{F}_{тяжести}} - \text{сила тяжести (H)} $$
$$ {{F}_{арх}} - \text{сила Архимеда (H)} $$
Законы сохранения
26) Механическая работа
$$\boxed{ {A} = {F \cdot S} \text{ [Дж]}}$$
$$A - \text{механическая работа (Дж)}$$
$$F - \text{постоянная сила, действующая на тело (Н)}$$
$$S - \text{перемещение в направлении действия силы (м)}$$
27) Мощность
$$\boxed{ {N} = {A \over t } \text{ [Вт]}}$$
$$N - \text{мощность (Вт)}$$
$$A - \text{работа (Дж)}$$
$$t - \text{время (с)}$$
$$\boxed{ {N} = {F \cdot V} \text{ [Вт]}}$$
$$N - \text{мощность (Вт)}$$
$$F - \text{постоянная сила, действующая на тело (Н)}$$
$$V - \text{скорость тела (м/с)}$$
28) Кинетическая энергия
$$\boxed{ {K} = {{m}\ \cdot v^2 \over 2 } \text{ [Дж]}}$$
$$K - \text{кинетическая энергия (Дж)}$$
$$m - \text{масса тела (кг)}$$
$$v - \text{скорость тела (м/с)}$$
29) Потенциальная энергия тела вблизи поверхности земли
$$\boxed{ {П} = {{m}\ \cdot g \cdot h } \text{ [Дж]}}$$
$$П - \text{потенциальная энергия (Дж)}$$
$$m - \text{масса тела (кг)}$$
$$g - \text{ускорение свободного падения (м/с²)}$$
$$h - \text{расстояние от центра масс тела до потенциального нуля (м)}$$
30) Потенциальная энергия сжатой пружины
$$\boxed{ {П} = {{k}\ \cdot \Delta x^2 \over 2 } \text{ [Дж]}}$$
$$П - \text{потенциальная энергия (Дж)}$$
$$k - \text{коэффициент жесткости пружины (Н/м)}$$
$$\Delta x - \text{величина на которую сжата или растянута пружина (м)}$$
31) Связь между работой и энергией
$$\boxed{ {Е} = {Е_{o} + А_{тр}+А_{внешн}} \text{ [Дж]}}$$
$$Е - \text{механическая энергия (Дж)}$$
$$Е_{o} - \text{начальная механическая энергия (Дж)}$$
$$А_{тр} - \text{работа внутренних сил трения (Дж)}$$
$$А_{внешн} - \text{внешняя работа (Дж)}$$
